Vamos conhecer um pouco sobre o trabalho de Euclides? Você pode nunca ter ouvido falar dele, mas o fato é que a forma como este geômetra apresentou suas construções geométricas foi tão eficaz, que mesmo que a régua não tenha nenhuma marcação e nem nada escrito nela, essas construções geométricas ainda são perfeitamente possíveis, usando régua e compasso. E ele mostrou isto cerca de dois mil e trezentos anos atrás!
EUCLIDES E “OS ELEMENTOS”
Antes de entender um pouco do pensamento de Euclides mencionado no parágrafo anterior, que tal descobrir um pouco sobre este personagem histórico? Euclides de Alexandria (como ficou conhecido por ter lecionado na Universidade de Alexandria) escreveu a mais renomada obra da história da matemática, uma série de 13 livros entitulada “Os elementos” (da qual o primeiro livro foi objeto de estudo da minha monografia de pós-graduação 🙂 ). Acredita-se que nenhum outro trabalho, exceto a bíblia, tenha sido tão largamente usado ou estudado como “Os elementos”, e também que nenhuma outra obra tenha exercido maior influência no pensamento científico! Porém, grande parte da geometria que Euclides usa em sua obra já havia sido desenvolvida por geômetras anteriores. Ué, como assim? Ele copiou dos outros? Veja bem: ideias matemáticas servem para serem usadas, certo? A partir da publicação de uma ideia, aquela ideia não é propriedade intelectual da pessoa que primeiro a publicou. Ela pode servir para outros fazerem novas descobertas ou outras abordagens usando aquela ideia. Nesse sentido, um dos maiores méritos de Euclides em seu trabalho foi ter conseguido organizar esses esforços anteriores em uma sequência lógica, onde a partir de conhecimentos mais simples, se deduzem outros conhecimentos.
Pronto, agora já podemos entender como funciona esse negócio de fazer construções geométricas apenas com régua e compasso, mas sem precisar das marcações da régua e nem de aproveitar uma abertura do compasso para transferir uma distância! Euclides mostra como isso funciona nas 3 primeiras proposições do livro I de “Os elementos”, que você pode ver mais abaixo nesta página, sendo que eu adaptei o texto da versão latina de Frederico Commandino de “Os elementos” de Euclides (disponível neste link), usando termos mais comuns na geometria moderna, em português do Brasil. Já as construções geométricas, eu as fiz usando um software de geometria dinâmica chamado C.a.R. (desenvolvido pelo professor René Grothmann da Universidade Católica de Berlim, na Alemanha), também conhecido como “Régua e Compasso”.
Na versão de Frederico Commandino de “Os elementos”, o texto contém referências a axiomas, postulados e definições escritas por Euclides, que não incluirei aqui (se quiser ler tudo na íntegra, é só clicar no link do parágrafo acima! Ha, e ir procurando no site por outros links para ir seguindo a leitura do livro). Porém, aqui na continuação abaixo deste parágrafo, eu substituí essas referências por algumas explicações adicionais, conforme achei necessário. Fiz alguns pontos com um formato quadrado nas construções com o C.a.R., apenas para simbolizar que esses pontos não são necessários para a construção geométrica, servindo apenas para nomear os elementos. É interessante observar que a proposição 2 usa o que foi feito na proposição 1, e a proposição 3 usa o que foi feito na 2. Ou seja, como eu já disse em outro parágrafo, elas são organizadas em uma sequência lógica. Aproveite agora, então, para se familiarizar com um pouquinho dessa obra, que nos dá um vislumbre das origens da geometria moderna!
CONHECENDO AS TRÊS PRIMEIRAS PROPOSIÇÕES DO LIVRO I DE “OS ELEMENTOS”
Proposição 1 (problema)
Sobre um segmento de reta determinado, construir um triângulo equilátero.
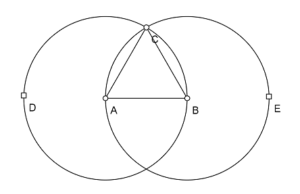
Seja o segmento de reta AB de um certo comprimento. Deve-se sobre ele construir um triângulo equilátero.
Com o centro A e com o intervalo AB como raio, se faça o círculo BCD; e com o centro B e com o intervalo BA como raio, se faça o círculo ACE. Do ponto C, onde os círculos se cortam reciprocamente, se tirem para os pontos A e B os segmentos CA e CB. O triângulo ABC será equilátero.
Sendo o ponto A o centro do círculo BCD, será AC=AB (pois ambos são raios do círculo). E sendo o ponto B o centro do círculo CAE, será BC=BA (pela mesma razão). Mas já vimos que CA=AB. Logo, tanto CA, como CB, são iguais a AB. Mas as coisas que são iguais a uma terceira, são iguais entre si. Logo será CA=CB. Assim, os três segmentos CA, AB e BC são iguais; e por consequência o triângulo ABC, feito sobre o segmento dado AB, é equilátero.
Proposição 2 (problema)
De um ponto dado, tirar um segmento de reta igual a outro segmento de reta dado.
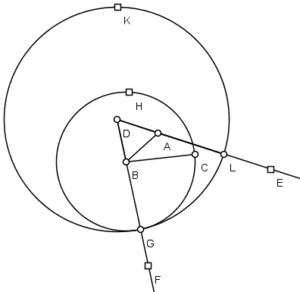
Seja dado o ponto A, e dado também o segmento BC. Deve-se do ponto A tirar um segmento de reta igual ao segmento dado BC.
Do ponto A para o ponto B tire-se o segmento AB, e sobre este se faça (pela proposição 1) o triângulo equilátero DAB; e se produzam as retas AE e BF na direção das retas DA e DB, respectivamente. Com o centro B e o intervalo BC como raio, se faça o círculo CGH com o ponto G sobre a reta BF; e com o centro D e o intervalo DG como raio, se faça o círculo GKL com o ponto L sobre a reta AE.
Sendo o ponto B o centro do círculo CGH, será BC=BG (pois ambos são raios do círculo). E sendo D o centro do círculo GKL, será DL=DG (pela mesma razão). Mas as partes DA e DB das retas DL e DG são iguais, pois são lados do triângulo equilátero DAB. Logo, tiradas estas, as partes restantes AL e BG serão também iguais (pois, se de coisas iguais se tirarem outras iguais, os restos serão iguais). Mas já demonstramos que BC=BG. Logo, cada uma das duas AL e BC, será igual a BG. Mas as coisas iguais a uma terceira, são iguais entre si. Logo será AL=BC; e por consequência tiramos do ponto A o segmento de reta AL igual ao outro segmento dado BC.
Elementos ocultos na construção: (os dois círculos cinzas, usados para construir o triângulo equilátero, marcando o ponto D onde os dois círculos se encontram)
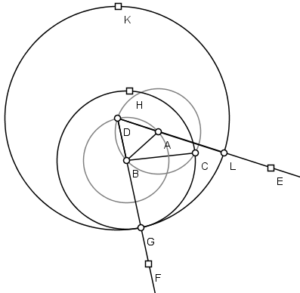
Proposição 3 (problema)
Dadas duas linhas retas desiguais, cortar da linha maior uma parte igual à linha menor.
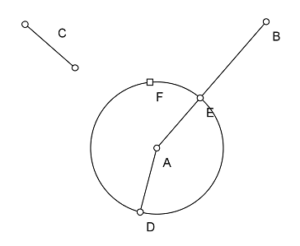
Sejam as duas retas desiguais AB, e c, e seja AB maior. Deve-se da reta maior AB cortar uma parte igual à reta menor c.
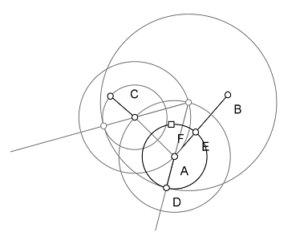
Do ponto A tire-se (pela proposição 2) a reta AD=c. Com o centro A e o intervalo AD como raio, se faça o círculo DEF. Como o ponto A é o centro do círculo DEF, será AE=AD (pois ambos são raios do círculo). Mas temos também c=AD. Logo tanto AE, como c, serão iguais a AD; e por consequência AE=c. Logo, tiramos da reta maior AB uma parte igual à reta c, que é menor que AB.
Elementos ocultos na construção:
É isso, espero que tenha gostado! “Os elementos” é um trabalho bem interessante. Apesar do seu domínio quase absoluto na forma como a geometria foi desenvolvida por mais de dois milênios, essa obra não trata apenas de geometria, como às vezes se pensa. Segundo Howard Eves, o assunto do sétimo até o nono livro de “Os elementos” é teoria dos números, e o décimo livro é sobre incomensurabilidade.
E aí, vai encarar? 😉
.
