Introdução
Quando pensamos em soma ou subtração entre frações de uma pizza, por exemplo, surge um problema quando as frações representam pedaços de tamanhos diferentes. Se João comeu ¼ de pizza e Maria comeu ⅛, então que fração da pizza eles comeram no total? Ora, ¼ da pizza é um pedaço maior do que ⅛. Porém, se dividirmos a pizza em oito pedaços iguais antes de João comer sua parte, então será fácil perceber que ele comeu dois oitavos de pizza. Não faria diferença para o seu estômago dividir a pizza em oito partes e comer duas, ou dividi-la em quatro partes e comer uma. Por isso dizemos que as frações “dois oitavos” e “um quarto” são equivalentes. Logo, é correto afirmar que João e Maria comeram, juntos, três oitavos da pizza. Ou seja, quando somamos frações com denominadores iguais, estamos juntando pedaços do mesmo tamanho, e aí fica fácil. Veja os exemplos a seguir:
- SOMA DE FRAÇÕES
Exemplo 1:
Quando os números de baixo (denominadores) são iguais, basta somar os números de cima (numeradores), e depois repetir o número de baixo, que era igual nas duas frações. Ou seja, no exemplo abaixo, somamos 5+4=9, e repetimos o número 6. Então, o resultado é a fração “nove sextos”. Mas não esqueça de simplificar o resultado, quando for possível dividir o numerador e o denominador por um mesmo número:
![]()
.
Exemplo 2:
Quando os denominadores são diferentes, devemos primeiro torná-los iguais, fazendo o M.M.C. entre eles. Considere a soma a seguir, onde alterei só o denominador da primeira fração do exemplo anterior:

Começamos fazendo o M.M.C. entre 9 e 6, que é igual a 18. Devemos então transformar as duas frações em frações equivalentes que tenham o denominador 18. Mas como?
Lembre-se que uma fração equivalente pode ser encontrada também multiplicando o numerador e o denominador por um mesmo número. Para que a fração “cinco nonos” se transforme em uma fração de denominador 18, precisamos multiplicar o 9 por 2. Sendo assim, multiplicaremos o 5 também por 2.
![]()
Já na fração “quatro sextos”, precisamos multiplicar o 6 por quanto para obter o denominador 18? Por 3, pois 6×3=18. Então, devemos multiplicar o numerador também por 3. (os dois precisam ser multiplicados pelo mesmo número, para que a fração seja equivalente)
![]()
Então, teremos:
![]()
.
- SUBTRAÇÃO DE FRAÇÕES
A subtração é feita de modo semelhante à soma. Veja os exemplos:
Exemplo 3:
Quando os denominadores são iguais, basta subtrair os numeradores, e depois repetir o denominador. Em seguida, simplificar o resultado, se for possível. Neste exemplo, o resultado não pode ser simplificado, pois 8 e 15 não têm um divisor comum:
![]()
Exemplo 4:
Quando os denominadores são diferentes, devemos primeiro torná-los iguais:
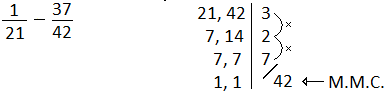
Como o M.M.C. entre os denominadores é 42, a primeira fração deve ser transformada em uma outra fração equivalente, que tenha o denominador 42:
![]()
A segunda fração da subtração já tem o denominador 42, então não devemos alterá-la. Voltando ao nosso cálculo inicial, teremos:
![]()
Observação: se você ainda não cursou o sétimo ano do ensino fundamental, aqui vai uma breve explicação da conta 2 – 37 que foi feita acima: como podemos tirar 37 de 2? Se, por exemplo, alguém tem duas balas, como essa pessoa pode perder 37 balas, se só possui duas? Nesse caso, podemos imaginar que a pessoa apostou 37 balas com alguém em um jogo, e perdeu a aposta. Ela terá que dar ao vencedor as duas balas que possui, e ainda ficará devendo 35 balas. Para representar essa dívida, podemos colocar um sinal de menos à esquerda do 35. Então, 2 – 37 seria igual a -35, que é um número negativo (que pode ser usado para representar uma dívida, por exemplo). Mas isto é assunto para o sétimo ano! Se você estiver no sexto ano, não se preocupe com isso agora, é apenas uma curiosidade.
.
