Olá! Aqui, o objetivo principal será compreender como podemos chegar às fórmulas de juros simples e compostos. Atingir essa compreensão requer uma boa dose de paciência para analisar com calma cada situação… mas creio que é um bom caminho para ficar mais familiarizado com o assunto. Para facilitar, o sinal de multiplicação aqui será definido como * (asterisco). Não esqueça, ao encontrar letras juntas sem nenhum sinal entre elas, que isto significa que elas estão sendo multiplicadas. Por exemplo, x y w é o mesmo que x * y * w. Bons estudos!
-
JUROS SIMPLES
Os juros simples, como o nome já diz, são mesmo bem simples. Se alguém empresta uma quantia cobrando juros simples, então a cada período de tempo pré-definido (mês ou ano, por exemplo), o devedor deverá pagar um valor fixo a mais, que é uma certa porcentagem do valor que tomou emprestado. Por exemplo, se alguém emprestar R$2000,00 cobrando juros simples de 10% ao mês, então deverá receber de volta seu dinheiro e, para cada mês que o devedor estiver com o dinheiro, mais R$200,00 (10% de 2000).
Perceba que geralmente não precisamos de uma fórmula para fazer esse tipo de cálculo. Se a pessoa levou, digamos, 4 meses para pagar, então deverá devolver os R$2000,00, e mais R$800,00.
ACHANDO UMA FÓRMULA
Mas e se nos depararmos com uma situação em que a fórmula possa ser útil? Como chegar a ela, sem precisar tê-la decorado?
Importante: para encontrarmos uma fórmula, geralmente é uma boa ideia pensar na conta que devemos fazer em cada situação, sempre partindo do valor inicial. E isso não serve só para juros. Em geral, essa é uma boa forma de se chegar a uma fórmula, para representar diversas situações na matemática.
Vamos primeiro definir as variáveis:
C → capital i → taxa de juros j → juros (em R$) t → tempo M → montante
No exemplo anterior, quais cálculos precisamos fazer para calcular o montante? Bem, se passou um mês (t = 1), os juros serão de R$200,00. Mas, para chegar a uma fórmula, precisamos pensar em todas as contas que estamos fazendo, inclusive o cálculo dos juros.
Bem, temos i = 10%. Mas lembre que:
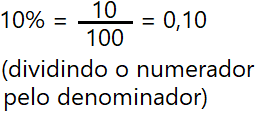
(caso tenha alguma dúvida sobre frações, acesse neste link uma página deste blog sobre o assunto)
Para calcular 10% de 2000, fazemos 0,10 vezes 2000. Ou seja, i vezes C. Isto serão os juros (j).
Então, se passou 1 mês (t = 1), temos:
j = 0,10*2000 (que dará 200)
M = 2000 + j ou M = 2000 + 0,10*2000 (que dará 2200)
Mas, se passaram 2 meses (t = 2), os juros serão de R$400,00, pois são R$200,00 para cada mês, então teremos que multiplicar os juros de cada mês pelo número de meses, para achar o valor total dos juros. Então, teremos:
j = 0,10*2000*2 (que dará 400)
M = 2000 + j ou M = 2000 + 0,10*2000*2 (que dará 2400)
Para t = 3, teremos:
j = 0,10*2000*3 (que dará 600)
M = 2000 + j ou M = 2000 + 0,10*2000*3 (que dará 2600)
Quando percebermos que este padrão continuará para t = 4, t = 5, etc, poderemos chegar às formulas dos juros e do montante, generalizando este cálculo para quaisquer situações de juros simples:
j = i C t
M = C + j ou M = C + i C t
Podemos também colocar o C em evidência na fórmula do montante, escrevendo-a na forma abaixo: (esse recurso facilitará o raciocínio para achar as fórmulas de juros compostos)
M = C (1 + i t)
.
-
JUROS COMPOSTOS
Os juros compostos NÃO são calculados sempre sobre o valor inicial, como vimos nos juros simples. Eles são calculados sobre o valor devido após cada período (no nosso exemplo, após cada mês, já que os juros são de 10% ao mês).
Assim, vamos considerar o mesmo exemplo, mas agora os R$2000,00 renderão a uma taxa de juros compostos de 10% ao mês. E vamos direto encontrar as fórmulas (sendo que usaremos, como já foi dito, o recurso de colocar o C em evidência):
ENCONTRANDO AS FÓRMULAS
Vamos lá! Como fica a conta em cada situação?
Se passou 1 mês (t = 1), temos:
j = 0,10*2000 (que dará 200)
M = 2000 + j ou M = 2000 + 0,10*2000 (que dará 2200)
ou, colocando o C (que é 2000) em evidência:
M = 2000 (1 + 0,10) ou M = 2000 * 1,10
Ou seja, é o mesmo cálculo que fizemos nos juros simples, para t = 1. A partir do segundo período (no nosso exemplo, o segundo mês) é que o cálculo mudará, pois os juros agora serão calculados sobre o valor devido (incluindo os R$200,00 de juros do primeiro mês). Portanto, para t = 2, teremos que adicionar, ao valor devido, 10% de R$2200,00. Perceba, porém, que a conta começará a ficar complicada. Veja:
j = 0,10*2000 + 0,10* (2000 + 200)
M = 2000 + j ou M = 2000 + 0,10*2000 + 0,10* (2000 + 200)
Faremos então este cálculo de outra maneira. Para isso, devemos perceber o que fizemos ao colocar o 2000 em evidência anteriormente: 2000 + 0,10*2000 é o mesmo que 2000 * 1,10. Ou seja, para adicionarmos a um número 10% dele mesmo, podemos simplesmente multiplicar esse número por 1,10 (que é 0,10 mais uma unidade e que, por isso, será escrito na fórmula como i + 1). Então, como teremos que adicionar, ao valor devido, sempre 10% desse mesmo valor, podemos fazer o cálculo do montante para t = 2 assim:
M = (2000 * 1,10) * 1,10
Ou seja, o valor devido após o primeiro mês (que é 2000 * 1,10) mais 10% dele mesmo. Mas, para somar a um valor 10% dele mesmo, como já vimos, podemos simplesmente multiplicar esse número por 1,10 (de novo).
Como nesse cálculo só temos multiplicações, não precisamos nos preocupar em colocar parênteses, então poderíamos escrever, para t = 2, M = 2000 * 1,10 * 1,10 ou M = 2000 * 1,102. Logo, seguindo o mesmo raciocínio, teremos:
Para t = 3:
M = 2000 * 1,10 * 1,10 * 1,10 ou M = 2000 * 1,103
Para t = 4:
M = 2000 * 1,10 * 1,10 * 1,10 * 1,10 ou M = 2000 * 1,104
Logo, a fórmula de juros compostos para calcular o montante após t meses (ou anos ou dias, dependendo da situação) fica assim:
M = C*(i+1)t
(lembre-se que 1,10 é i+1, ou seja, a taxa de juros 0,10 mais uma unidade)
Quanto à fórmula para calcular os juros, sabemos que M = C + j. Daí temos que M – C = j. Então, podemos escrever:
j = M – C ou j = C*(i+1)t – C
Desafio: Um esquimó emprestou 1 kg de sorvete de menta ao seu colega. Depois de dois meses, o colega bate à porta do iglu onde mora o esquimó, dizendo: “Muito obrigado, aqui está 1 kg de sorvete, que acabo de fazer!”. O esquimó, muito avarento, respondeu: “E quanto aos juros? Você me deve mais 210 gramas de sorvete!”.
1a parte do desafio: Caso o esquimó avarento tenha pensado em juros simples, qual a taxa de juros que ele cobrou ao mês?
2a parte do desafio: E se ele tiver pensado em juros compostos, qual a taxa de juros que ele cobrou ao mês?
.
